Abstract
The original work by Francis Galton on mean reversion in 1886 emphasized relative before absolute, talked about the relation of the variable with the sample average, pointed out the balance between convergence and divergence and showcased cross-domain expression of mean reversion. Though mean reversion as an idea has been in the open domain for 130 years, there has been no attempt to extend the Galtonian definition of natural systems into a framework that could allow for better understanding and functioning of natural systems and also explain the failures of reversion. Any proxy that expresses Galtonian reversion should be simple, relative and universal. This paper takes a stock market case and defines a framework that builds on the Galtonian explanation of a natural system and incorporates the idea of relative ranking, relative average, balancing forces of convergence and divergence, and the universal workability of the framework across domains.
Galton’s ‘Relativeness’
Most of Galton’s work talks about relativeness, either in the form of comparisons, ratios, deviations, proportions, degrees, scale, extremes etc. Rather he goes about giving relativeness more importance than absolute values. Even deviates (deviations) are referred too in context of comparisons between the height of offspring and comparisons between parent and offspring stature. The focus is not on the absolute values of the median but how they are relatively shifting towards average (mediocrity). Degrees of inheritance of degrees (from parents or ancestors) are also calculated in terms of proportions. He even calls the idea of regression, as the average ratio of regression and generational continuity of such a statistical proportional relative ratio.
‘The law that I wish to establish refers primarily to the inheritance of different degrees of tallness and shortness, and only secondarily to the absolute nature. That is to say, it refers to the measurement made from the crown to the level of mediocrity, upwards or downwards as the case may be, and not from the crown of the head to the ground.’
‘It is that the height deviate of the off spring is, on average, two-thirds of the height – deviate from it’s mid – parentage.’
‘It will be seen that the relations between the statures of the children and their mid – parents, which are perfectly simple when referred to the scale of deviates at the right hand of the plate, do not admit of being briefly phrased when they are referred to the scale of stature at it’s left.’
‘It is easily to be shown that we ought to expect filial regression, and that it should amount to some constant fractional part of the value of the mid-parental deviation.’
‘The child inherits partly from his parents and partly from ancestry.’
‘The process throughout is one of proportionate dilutions, and therefore the joint effect of all of them is to weaken the original wine in a constant ratio.’
‘The average ratio of regression.’
‘One generation was succeeded by another that proved to be it’s statistical counterpart.’
Regression towards mediocrity in Hereditary Stature, Galton, 1886
Galton’s Reversion
Reversion was what intrigued Galton. The further away the natural data went from the mean the stronger it was to revert. The rule was simple; positive extreme was prone to revert down, while negative extreme was prone to revert up. Even here there was a sense of relativeness to the mean, to mediocrity, as he referred to it. Regression got a bigger weight than deviation, though deviation was an integral part of the reversion. There was no reversion without deviation and vice versa. The phenomenon took more importance, so much so that the degree of lack of resemblance in stature of the offspring from their parents was ascribed to the law of reversion. Convergence was more of focus than divergence.
‘The mean filial regression towards mediocrity was directly proportional to the parental deviation from it.’
‘It appeared from these experiments that the offspring did not tend to resemble their parent seeds in size, but to be always more mediocre than they – to be smaller than the parents, if the parents were large; to be larger than the parents, if the parents were very small. The point of convergence was considerably below the average size.’
‘The law is even handed; it levies the same heavy succession tax on the transmission of badness as well as goodness. If it discourages the extravagant expectations of gifted parents that their children will inherit all their powers, it is no less discountenances extravagant fears that they will inherit all their weakness and diseases.’
Regression towards mediocrity in Hereditary Stature, Galton, 1886
The table here explained how at the top extreme, the medians of the adult children (last column) were 72.2 lower than the heights of the mid parents 72.5 (First column). And how at the bottom extreme, the medians of the adult children (last column) were 65.8 higher than the heights of the mid parents 64.5 (First column).
Top Extreme 72.5; Bottom Extreme 64.5
Galton’s cross-domain cases
Galton tested and proved reversion in height, and seeds, a cross-domain expression for reversion. Now the idea has universal application in Finance, psychology, etc.
Galton’s natural system
Galton classified his system as organic. There was constancy in values, proportion, and ratios. There was a succession, continuity, and periodicity from one generation to the other. There was a context and extremes in the data set studied. There was more proportionality than equality. Rather lack of equality between tall parents leading to tall children was the basis of the framework. There was dynamism between the data sets, increasing and decreasing change, accelerating and decelerating change. There was a centre for a generation, which was relative to the data. Despite the difference and change, the pattern persisted and balanced out, reached a state of equilibrium, compactness. There was a context of top and bottom. There were opposing actions; dispersive and converging forces, opposing tendencies, spring like action. There was a process of transformation generationally, a process of replacement by the data set to freshen itself up, a sequence of stages. Despite the order there was a sense of randomness, less scattered data lead to more scattered data and vice versa.
‘How is it, I ask, that in each successive generation there proves to be the same number of men per
thousand, who range between any limits of stature we please to specify, although the tall men are rarely descended from equally tall parents, or the short men from equally short? How is the balance from the other sources so nicely made up? The answer is that the process comprises two opposite sets of action, one concentrative and the other dispersive, and of such a character that they necessarily neutralise one another, and fall into a state of stable equilibrium. By the first set, a system of scattered elements is replaced by another systems which is less scattered; by the second set, each of these new elements becomes a centre whence a third system of elements are dispersed.’
‘The hypothesis of organic stability.’
‘In the first of these two stages we start from the population generally, in the first generation; then the units of the population group themselves, as it were by chance, into married couples, whence the more compact system of mid-parentages is derived, and then by a regression of the values of the mid- parentages the still more compact system of generants is derived. In the second stage each generant is a centre whence the offspring diverge upwards and downwards to form the second generation. The stability of the balance between the opposed tendencies is due to the regression being proportionate to the deviation. It acts like a spring against a weight; the spring stretches until it’s resilient force balances the weight, then the two forces of spring and weight are in stable equilibrium; for if the weight be lifted by the hand, it will obviously fall down again when the hand is withdrawn, and if it be depressed by the hand, the resilience of the spring will be thereby increased, so that the weight will rise when the hand is withdrawn.’
Regression towards mediocrity in Hereditary Stature, Galton, 1886
Galton’s divergence and Outliers
Galton’s reversion is connected to the dispersion in the system. The both forces act together to keep the dynamism going. The data studied also studies extremes of heights, classifying levels as above the top height and below the low levels. Galton’s case is based on these Above Top and Below Bottom readings, but still he does not delve much on reasons for divergence or extremities in general. His focus is primarily on divergence from mean rather that top or bottom rankings.
The number of individuals in a population who differ from mediocrity is so preponderant that it is more frequently the case that an exceptional man is the somewhat exceptional son of rather mediocre parents, than the average son of very exceptional parents.
Regression towards mediocrity in Hereditary Stature, Galton, 1886
Galton’s regularity, durations and connection between dispersion and reversion
Galton’s considered reversion as extremely regular, leading to a state of constancy. Regularity meant that reversion and dispersion followed a cyclical process. He talked about an alternation between the two. The time durations Galton considered were generational and hence were more discrete rather than continuous in their expression. Galton observed or focused on a complete cycle from one generation to the next, from dispersion and reversion rather than a multiplicity of cycles. This is why his conclusion regarding unchanged states, a kind of completion, which was necessary for him to showcase the phenomenon of reversion, and the constancy in it.
‘The statistical variations of stature are extremely regular, so much so that their general conformity
with the results of the calculations based on the abstract law of frequency of error is an accepted fact by anthropologists.’
‘Until the step by step process of dispersion has been overtaken and exactly checked by the growing antagonism of reversion.’
‘Reversion was like an elastic spring. “Its tendency to recoil increases the more it is stretched, hence equilibrium must at length ensue between reversion and family variability.’
The table above explains one cycle of concentration and dispersion.
Galton’s limitations
Though Galton talked about divergence being an essential part of the reversion behavior, he did not focus on the quantification of divergence. The reason could be the scope of his research back in 1886, which was about bringing out the law of reversion (focus on mediocrity). There could have been other reasons why divergence was out of the scope for his research. Galton’s data set had limitations when it came to defining or studying divergence.
Galton’s reversion scope also seem limited to the process ending in reversion as a completing process rather than understanding the changing dynamics between reversion and dispersion. He limited his case of dynamics between reversion and dispersion to alternating cycle of reversion and dispersion, and did not focus on the explanation of divergence or on multiple durations of periodicity. The quality of the data set also restricted him from testing various periodicities and the inGluence of periodicity on reversion. For Galton it was the balance between the two, with regression being the order and divergence the disorder generating process. No Gluctuations, potential failures in the periodicity were considered. Rather Galton considered the process extremely regular.
Today we know that mean reversion as a law though robust is prone to failure. Time varying uncertainty has challenged the robustness. The case of divergence has gone stronger since then, now that we have ubiquity of the power law expression. Galton’s definition of extremes as an intrinsic case for reversion (above, below denomination for his stature bins) was also a limitation in dealing with outliers; mean as we know is also inGluenced by outliers.
Galton's explanation for the regression phenomenon he observed is now known to be incorrect. He stated: “A child inherits partly from his parents, partly from his ancestors. Speaking generally, the further his genealogy goes back, the more numerous and varied will his ancestry become, until they cease to differ from any equally numerous sample taken at haphazard from the race at large.” This is incorrect, since a child receives its genetic makeup exclusively from its parents. There is no generation skipping in genetic material. Any genetic material from earlier ancestors than the parents must have passed through the parents. The phenomenon is better understood if we assume that the inherited trait (e.g., height) is controlled by a large number of recessive genes. Exceptionally tall individuals must be homozygous for increased height mutations on a large proportion of these loci. But the loci, which carry these mutations, are not necessarily shared between two tall individuals, and if these individuals mate, their offspring will be on average homozygous for "tall" mutations on fewer loci than either of their parents. In addition, height is not entirely genetically determined, but also subject to environmental influences during development, which make offspring of exceptional parents even more likely to be closer to the average than their parents.
Mean Reversion Failure
As expected future researchers not only challenged the robustness of the universal framework of mean reversion but also pointed out gaps in it. Mean reversion failure is about all the cases where mean reversion does not happen in a specified period. Since reversion to mean is assumed to have nothing to do with time, anticipating a reversion is a fixed time is considered a normal behavior. When the reversion does not happen, it’s considered a case of mean reversion failure.
Galton’s fallacy on the other hand is a case pitted against mean reversion as a natural phenomenon. The fallacy is about ascribing a cause where none exists and could be just because of natural Gluctuations. Regression itself does not refer to causality, but research abounds challenging the idea under grounds of unreasonable causality or failing to manifest. Despite all the failures and fallacy, mean reversion remains a universal law, which has cases in every natural system, be it Financial, non- Financial, behavioral or simply web data.
Though Pareto (1848) and Galton (1822) were contemporaries, there work seems far from connected. Galton was behind the regression in mean, mean reversion and ideas like the bean Machine also known as the quincunx or Galton box, with which he demonstrated the central limit theorem, in particular that the normal distribution is approximate to the binomial distribution. While Pareto was behind the popular Pareto curve drives the 80-20 principle and also is a part of the power law, the phenomenon seen widely in nature. Both Pareto and Galton’s work was important because they talked about an observed phenomenon in society. Just like power law, we still see mean reversion expressing in multiple domains. Without any explanation how and why the two natural expressions could be reconciled and we don’t need to trash one to embrace the other.
Mean reversion failure is a market reality. Still owing to it’s universality the investment management business relies on mean reversion strategies. Momentum follows reversion cyclically. Behavioral Finance cited mean reversion to challenge the assumption of randomness in efficient market hypothesis. Statistics also proves that 90% of fund managers fail to beat the market consistently.. Hence understanding mean reversion, its reality and failures is important for investment managers.
Ideal mean reversion. This is how markets should express mean reversion. The overbought (overvalued should push back to an absolute mean and vice versa.
However many times after falling below mean markets don’t revert back to the absolute mean. While sometimes after getting oversold (overvalued) and staying above the mean attempting to get back to mean value, markets or asset prices stay overbought and get more overbought (overvalued). Sometimes there is a clear disregard to mean value, markets ignore the mean totally.
Mean Reversion Framework and Natural Systems
The universality of reversion can not be restricted by nature and characteristic of a natural data set. So a mean reversion framework should be scalable for any natural system. This means it should be simple, relative, universal in its behavior and have scalability across different time durations. Universality also means that the framework should consider both divergence (dispersion) and regression in the same unified framework. Understanding and quantifying divergence is a pre step to combine divergence and reversion.
Markets with all regions, assets, components are a dynamic systems. Different groups have different Glight, there own dynamics, be it a pure group on currency, a pure group on the Dow 30 stocks, a group of top regional indices etc. or a group created from world wide web date like Google trends.
Any dynamical system can be understood by data mapping. Even stock market groups can be understood by data rankings. Different groups would have different character. Understanding components would require understanding the group they belong too. Any selection approach from a group is incomplete without the understanding of the group. A group may have different speed, different volatility, different altitude, different spread etc.
After one understands the group specifications one can look at universal rules to understand how the group is moving, and where is it headed. Despite the randomness, there is an order. The group components are interconnected with seasonality of outperformance and underperformance. The group components exhibit divergence between the best and worst. This divergence is cyclical. Best underperformers could become worst and vice versa. This gives an illusion of oscillation around some absolute mean, a kind of statistical mean reversion. And all this dynamics is happening simultaneously at all degrees of time in a hierarchal multi temporal nested structure. All groups have different mean values, different extremes and different future course and behavior; the behavior can express irrespective of different risk types, preferences, classification or specification of the group; the behavior retains despite the degree of time.
Divergence as a case of failure of Mean Reversion
Divergence however we may refer to it, as dispersion, diversity, Gluctuation etc. is a law of nature and just like reversion is witnessed in all natural data sets. This is how nature and society works.
The whole idea of change is built around the dynamic movement of divergence and reversion. The need for balance comes from the constant push towards imbalance. Which suggests that reversion itself can not be assumed to be reaching in a state of constancy. The natural system is in a constant move between reversion and diversion. A constancy, as a state of utopia, is a static perspective of an underlying ever-changing dynamic system.
Philip Ball talked about suckers and collaborators in corporations. How at a certain time in the corporation, there are more collaborators, there is higher growth, when the suckers start to feed and inefficiency increases. At a certain point, the suckers outnumber the collaborators (the doers, the givers) and slowly the profits fall, there is little to share and it's then when collaboration comes back. This cyclicality, or movement from divergence to reversion drives the growth and decay in natural system, an essential driver of life.
Divergence is a part of all natural systems. It’s both inter and intra domain, process that drives natural variables from growth to value or vice versa, a process that powers momentum and reversion in natural variables, be it price, sentiment etc.. A universal law working across different time durations. The reason why natural systems witness outliers, extremities, and the reason why the same natural variables are brought back in balance by reversion. In some natural contexts we call this balancing events as an economic or social crisis.
How do we understand Divergence? When does it get weaker or stronger? How do we measure the balance between the two forces of divergence and reversion? How do we measure extremities? How can the natural system address complexity and be simple also? Natural systems are intrinsically complex, but simple in their functioning. Herbert Simon, defined complexity in his paper on Architecture of Complexity, 1962.
Complexity is intrinsically simple and hierarchal. Herbert Simon
Divergence Fallacy
Divergence is not considered quantifiable, but more of a random error because it is as ubiquitous as reversion. Something divergences are so prominent, regular that it has a high chance to be labeled as noise rather than something ordered. But divergence is the way nature and markets function and assuming divergence to be noise is like labeling nature as a Gluctuation.
There is more than a scientific evidence to disprove the random case for divergence. Divergence is a universality and if universal laws demonstrate order, then divergence should also have an order like reversion, or there should be a framework to explain the two together.
Data interpretation is an evolving science. Mean was a measure to understand data, a measure of central tendency. As time passed and data interpretation came off age, the size, quality and quantity of data enhanced. There was more data to understand, a lot of data. At some stage the attention shifted from data to divergence in data and expressions of divergence increased.
Analysts, economists, technicians have traditionally been studying and looking at price spreads and divergence for a long time. The spread between economic data, or between traditionally correlated assets. Over a period of time high correlations between assets prices have given way to poor correlation.
Clifford Pickover in, the math book, points that “Simple computer programs, which attempt to find regularity in sequences, may not see the regularity in Champernowne’s number30. This deficit reinforces the notion that statisticians must be very cautious when declaring a sequence to be random or patternless.”
Divergence, an illustration
The illustration explains the divergence between two price time series, the S&P 500 and the DOW 30 from 1991 to 1995. The green line is the divergence, which reached a high of 6% and kept falling secularly down till -33% in 1997. Over 6 years this was an annual premium of 5.5% in S&P over DOW. One could have tried anticipating divergence from 1997 using various technical, fundamental and statistical approaches.
However, it was hard to predict how the divergence is going to behave from 1997 to 2001. The divergence left the low band of positive 10% to – 33% during 1991 – 97 to + 50 - - 50%. The Gluctuation seemed tough to predict or anticipated. Technicians have long focused on anticipation of a price, but anticipating divergence is a bigger challenge. It’s like predicting not only momentum and reversion, but their respective degrees. After 2001 the divergence kept falling down till Oct 2003 where the historical premium of S&P 500 vs. Dow Jones industrial turned to a discount of -60%. This was a spread of 120% from 1999 divergence top till Oct 2003. Divergence remained in a negative and low range till Oct 2007 and DOW continued to stay at a premium vs. S&P.
Divergence, a case of relative Performance
Relative performance is the ratio of two diverging converging time series. Relative performance in stock market terms is the price performance of one asset netted against performance of another asset. The two compared assets can be a stock against its Index, a sector index against another sector Index, a portfolio against the composite index etc. Relative performance can also be understood as alpha. A negative relative performance is underperformance while a positive relative performance is outperformance.
Relative Performance of variable A vs. Variable B = (Value of Variable A on time n)/ (Value of Variable A on time n-1)-(Value of variable B on time n)/ (Value of Variable B on Day n-1)
The direction of Relative performance growing and decaying can suggest whether the diverging premium between any two variables (or asset prices) is increasing, decreasing or stagnating. This is an efficient way to quantify the spreads, first step to quantify a divergence visual, but still not enough to anticipate to direction of the divergence. This quantification still can’t anticipate direction in different degrees of time.
It means it can’t answer will S&P 500 continue to outperform DOW Jones industrials for the next 5 years. Why is it important to understand that Variable A will outperform Variable B for the next 5 years and then it’s going to reverse performance for the next 10 years?
It’s not just is weather but in many other areas of study that long term prediction are considered hard. Edward Lorenz small changes can be assumed to interfere with long term forecasting. There is always a timing constraint which interferes with long term forecasting. Long term prediction has a lot of economic value, a value that can be the difference between a society taking proactive steps to prosperity by managing risk.
The left hand chart illustrates daily Rate of Change over daily return prices and the right hand chart illustrates RP relative performance and a smoothed rate of change indicator (ROC).
Relative performance change; The results are the daily change in relative performance for Alcoa. This looks like a stochastic process. Smoothened daily change in relative performance; A 60 period averaging is done for the data. When smoother for a quarterly duration, the stochastic process starts to show a tendency.
Divergence, a case for relative performance cyclicality
The case for relative ranking is essential for the mean reversion framework as it allows for multi domain testing, testing across different periodicities, allows to study the behavior of a data set (group), allows for both static and dynamic comparison.
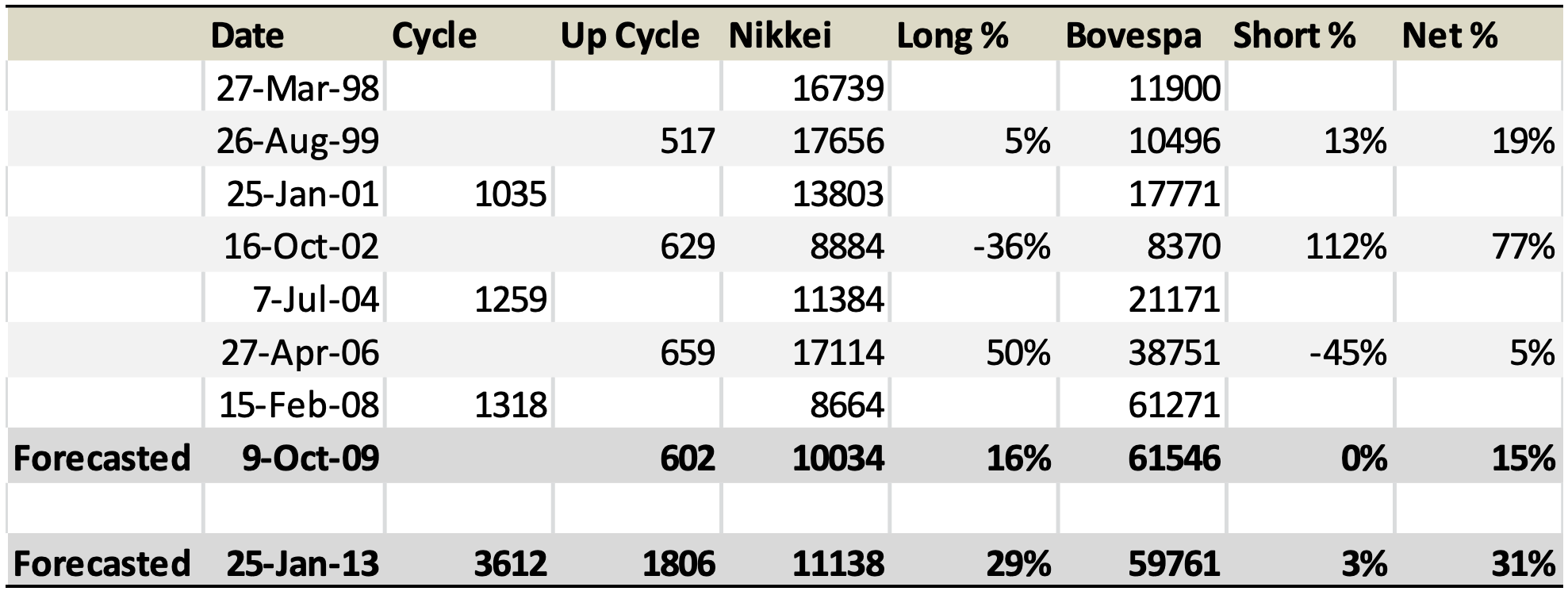
In building the case for a relative proxy and looking for common universal patterns, the previous paper on ‘The BRIC Model from a Japanese Perspective’, (2010; Pal, Nistor) studied the relative pair performance between the BRICs countries and Nikkei, based on three 36-40 month time horizons in the 10 -12 year larger economic cycle was studied. A rate of change indicator (ROC) was calculated for the relative ratio of the different stock market benchmark pairs. The ROC not only behaved as a performance cycle over the long term (10-12 years) and short term (36-40 months) but could also bring objectivity in looking at relative pairs (outperformance and underperformance) like Brazil Bovespa vs. Indian Sensex. The findings suggest that the longer (10-12 Year) and shorter performance cycles (5-6 Year Cycles) worked together and ROC on relative performance ratio lines could identify performance cyclicality. Jiseki was the Japanese term used for performance cycles.
The paper brought about the idea of the potential for objectivity while studying long-term relative performance (pairs) between various stock market benchmarks beyond causal inference. The performance between pairs had both diversion and reversion, but despite the periodicity and exogenous factors, the process lent itself to some objective quantification.
Table.– N225 vs. BVSP pair positive returns validates performance cycle time projections
Extending Relative Performance between a pair to a group, Divergence cyclicality
In another paper, ‘The Divergence Cyclicality’ Pal, Nistor 2010, the authors explained how grouping assets and ranking them could understand performance divergence. Divergence cyclicality could not only harness reversion and divergence, but also extend the case for quantifying relative pair performance. The paper discusses long-short cases between best and worst ranked assets and creates a divergence cycle indicator to pin point performers and underperformers in a case of global assets. The paper empirically showcased how divergence cyclicality could be used to understand performance divergence in markets. And since divergence is ubiquitous, the divergence cyclicality could be a good proxy for the natural growth and decay process across natural systems, witnessed through the respective data sets. Divergence cyclicality conceptually extended the idea of natural systems that not only expressed reversion, but extreme(s) reverting back to a relative mean.
Does the Relative Asset performance ranking change? Yes it does, here ranking from two periods are displayed. Period 1 top ranked assets fall in rankings in period 2. and bottom ranked asset from period 1 rise in ranking in period 2. The change is shown in the rankings in the third image. The rankings below are between global equity indices. DJIA (DOW 30) was the bottom ranked asset in period 1 . It moved up in rankings in period 2. The relative ranking of assets are benchmarked against S&P500.
Does the Relative Asset performance ranking change if one looks at a different asset class? Yes. Even if one looks at a new set of assets, the ranking from two periods show clear movement. Period 1 top ranked assets fall in rankings in period 2 and bottom ranked asset from period 1 rise in ranking in period 2. The change is shown in the rankings in the third image. The rankings below are between various metals. Silver moved from top ranking to bottom ranking, while Palladium moved from third best ranking to the top ranked metal in period 2. The relative ranking of assets are benchmarked against Gold.
The oscillator for Bank of America (BAC) indicates outperformance against DJIA (Dow) if the oscillator turns up and vice versa.
We have tabulated seven turn points. From 17 July 08 to 02 Sep 2008 (arrow 1 to 2) BAC outperformed DJIA by 42%. Similarly when the oscillator turned down (arrow 2 to 3), BAC underperformed DJIA by 108%. All the cases are illustrated above in the Figures above. The table below carries individual performance and net performance between the two assets.
Extending Divergence Cyclicality to a Proxy, Dynamic mean means Relative mean
What is a statistical average? Starting from the average salary, to the average rate of monsoon, to the average of Dow Jones Indices, averages are not only ubiquitous but they are part of popular psyche. Now, this is where the problem begins. An early meaning of the word average is "damage sustained at sea". An average was about assessing an insurable loss linked to a damaged property. Society loves status quo and hence the benchmarks that come with it.
Reality is far diverging from an average, averages are moving and have life, are dynamic and not static. The black swans, the outliers, the freak accidents, the successive luck, the toss of a long sequence of heads in a toss, the fat tails are just too frequent to keep challenging the illusion of an average.
This is why the average compensation, the average lifespan, the average monsoon, the average temperature, the average portfolio return are poor measures of group tendency, which is a tendency of the group components to move ahead in time, creating new extremes and a new mean.
Reality is far diverging from an average, averages are moving and have life, are dynamic and not static. The black swans, the outliers, the freak accidents, the successive luck, the toss of a long sequence of heads in a toss, the fat tails are just too frequent to keep challenging the illusion of an average.
This is why the average compensation, the average lifespan, the average monsoon, the average temperature, the average portfolio return are poor measures of group tendency, which is a tendency of the group components to move ahead in time, creating new extremes and a new mean.
Jiseki, performance cycles used in the BRIC paper built the case for divergence cycles using relative percentile ranking. Positive extreme is 100 percentile; Negative extreme is near 0 percentile;
While dynamic mean rests at 50. Every recorded value is relative to the group components. The universe is the group. And the mapping of ranking scores is for the group components. The ranking remains from 100 to 0. But the selections which register that value keep changing dynamically. What makes it to above 80 can be a different list of selections for different periods
What makes it to below 20 can be a different list of selections for different periods. What touches 50 moving down from 80 can be a different list of selections for different periods. What touches 50 moving up from 20 can be a different list of selections for different periods.
Disadvantages of reversion built around statistical mean; 1) Absolute mean is sensitive to extreme values; 2) Absolute mean is suitable for a certain time series type of data, but markets deliver over multiple time periods. 2) Absolute mean works when weights are equal, yet often investing requires unequal weights.
How dynamic mean overcomes the drawbacks of statistical mean; dynamic mean accommodates for
all the weaknesses of an absolute average mean based on a group of assets whether the group is large, small, equal weighted, unequal weighted...with or without outliers. Applicable to multiple investment time frames relative mean which change as the defined group changes or is redefined.
Dynamic Ranking, Time Durations and Jiseki
Ranking decreases in value suggesting a drop in relative performance of the component among it’s group, a decay process. The lower illustration is the opposite case of growth (increase) in rankings.
In an SSRN paper on relative strength and portfolio management, John Lewis explains how working with relative momentum (buying strong above average performers) strategy is good for a three- to six-month period but not good for one month and larger periods above nine months. For longer periods buying above average performers (outperformers) fails.
The risk metrics are driven by our Jiseki Time cycles, which are seasonal patterns of strength or weakness in assets. They are derived from percentile rankings from 1 to 100. The higher the percentile more the chance for an asset to weaken and worst the ranking, better the chance for the respective asset to outperform. 100 is top relative performance and 1 is worst performance. The idea is that performance is cyclical. A top performer will underperform in future and vice versa.
A top relative performer is also the worst value pick and the top relative underperformer is the best value pick. Jiseki is another name for Performance cycles, time triads and time fractals. The signals are illustrated as a running portfolio and as Jiseki Indices. These signals can be used by fund managers for relative allocations, traders for leverage bets and high net worth clients for selective trades. Jiseki Interpretation. Signals are interpreted as crossovers between various Jiseki Cycles. All three Jiseki cycles (Jiseki 1,2 and 3) depict different time frames. Example: An asset is ranked above 80 percentile and all the three Jiseki cycles are pointing lower, this suggests a running SHORT SIGNAL. Our Jiseki Indices use different kind of exits based on price and Jiseki Cycles. We have color coded the (Jiseki 1>Jiseki 2) SHORT zones with brown sandy (burlywood) and grey (Jiseki 1>Jiseki2) for LONG SIGNALS.
Natural Systems and Extreme(s) Reversion
Extreme(s) are prone to reversion. Extremes are about divergences and reversion is about seasonality and cyclicality. Divergence as we explained before could be expressed as a case for relative performance in a spread between two or more variables as a part of a group. Groups have extremes. The extreme exaggerates as the group size increases, larger the group, more intense the extreme and the more intense the extreme, the sharper the recoil reversion, which continues till the existence of the natural system. Extreme reversion financially can manifest as value or growth. The odds against or in favor classify an extreme. There is natural balance (behavior) connected to the extremes.
Herbert Simon’s bounded rationality, suggests that human rationality is bounded by the access to information. This idea can be extended to the data groups. As we create a group we bound the information in that group and hence limit what information could effect the inter group dynamics i.e. the interaction of components within that group. If we change the group, we change it’s information bounds, it’s character and hence it’s behavior. So ‘Group’, a proxy for information inGluences data mining and component selection from within the group. Since Jiseki rankings of a group is a sample expressing data universality, the ranking set can also express the distinct regimes in a natural system.
Thrashing “herding” behavior; The thrashing “herding” behavior witnessed in universal systems are similar to the near 0% and near 100% rankings of Jiseki Group where winners and losers.
The information is less than threshold needed as losers suffer from lack of interest, lack of trading volume, there is no interest from media and hence rejection (herding) of losers. The losers remain subdued and don’t emerge, revert till the information threshold breaks. Small sponsors of trends accumulate the worst losers, pick up contrarian stories, and gradually push the information above threshold. The more than 80% ranked components are so much positive that there is negative information that makes it to media. Winners are worshiped but at some stage buying or positivity exhausts and the momentum exhausts as the information threshold is breached as components rankings push lower sub 80%.
Order; as components move out of extreme winners (> 80%) or losers (< 20%) rankings owing to the increase information threshold, order comes in. The reversion from top and bottom leads to momentum. As sponsor and the smart money gathers size. The initial agents trigger the search for more information increasing popularity for the ongoing momentum trend (up or down). There is more order after the herding.
Random behavior; As components in momentum pushes to the 40 – 60% median relative range (from > 80% or from < 20%) leaving the information threshold behind, the lack of information now becomes too much information, leading randomness and disorder. Will the momentum continue? Will the reversion happen? This is the second behavior of a universal system.
According to the 2004 paper on Universality in Multi-Agent Systems; H. Van Dyke Parunak, Sven Brueckner Altarum Institute; Robert Savit; Dept. of Physics, University of Michigan, the authors said,
“we hypothesize that these regimes will not appear for truly optimizing decision-makers, since an optimal decision by definition uses all of the relevant information available. however, such processes are rarely encountered in practical real-world domains. real-time constraints impose time limits that effectively turn even an optimizer into a bounded rationalizer when confronted by large enough amounts of information.”
The authors conclude that it’s hard to make optimal decisions because of real time constraints which impose time limits. Moreover bounded rationality forces decision makers to be stuck in their situations. Translating this to the Jiseki Group Rankings a decision maker could be like a stock component in the 40-60 % rankings; < 20 or >80 % rankings restricted by it’s situation to move out it’s bound.
However when we look at a data universality from an extreme reversion framework, we have a framework that connects seasonality, outliers, and different degrees of time with variable growth and decay. Because of this Jiseki proxy could offer a behavior map to understand or navigate a preordained map moving from one ranking to another or from a random state, to an ordered state, to a herding state in a certain order. Jiseki proxy rankings offer a continuity between states, a kind of behavior map evolving in time.
Data Universality extends universality because it also assumes a leader – follower relationship, or a divergence - reversion relationship from the stage of transition you are looking at the system. The leaders have expression and an initiative to break the threshold, trigger a phase transition. The leader is just like that first molecule that heats up and triggers a phase transition. The leader could do it consciously or it could be a random initiative, which owing to it’s appropriate temporal stage inGluences the followers. Whether the leader understands the time constraint or is lucky to be there the leader outperforms the follower. The universality drives natural systems.
The 2004 paper also suggests that strategy and preference does not change the universal nature or the three stages a universal system goes through, random, herding and ordered.
Extreme Reversion, Jiseki Case
Assuming Jiseki is a proxy for natural systems, it should express the reversion and divergence behavior as explained by Galton. The Jiseki ranking is split into three bins; the 0-20 value bin (V); the 80-100 growth bin (G) and the core(transition, middle) bin (C) from 20-80.
According to Galton, the extremes tend to reverse. This means both the value (V) and Growth (G) bin should express reversion. And since divergence is a needed requirement or an expected balancing force, the rankings around the middle 50 ranking should express divergence. A stock market case study was tested for reversion and divergence. The FTSE UK (F) 100, Nikkei 225 Japan (N), STOXX 50 (S), STOXX Bank Sector (SB), S&P 100 (U) components were tested for 15 years of data for 20,40, 60, 125, 250, 500, 750, 1000, 1250, 1500, 2500, 3750 days. The stock prices were ranked on a quarterly performance and ranked on a scale of 0 to 100 and then tested for first) Absolute percentage of components moving from 0-20 Value bin to 80-100 Growth bin and percentage of 80-100 component bins moving from 80-100 ranking bin back to 0-20 Value bin. This was a test for extreme reversion in the Jiseki Proxy. Second) the Jiseki ranking from 40-60 (a part of the core (C) bin) was tested for divergence from average 50 rankings back to 0-20 Value and 80-100 Growth bin. The results confirmed reversion and divergence.
Table; Absolute Percent changes in the Jiseki Value components(0-20 proxy rankings) moving all the way up to 50 rankings and higher, depicted as % V > 50. And absolute Jiseki Growth components (80-100 proxy rankings) moving all the way down to 50 rankings and lower.
Table; Absolute percent number of Jiseki components(40-60 proxy rankings) moving all the way up to Growth (G) 80-100, depicted as % C to G. And percent number of Jiseki components (40-60 proxy rankings) moving all the way down to Value (V) 0-20, depicted as %C to V.
The illustration above is a summary of the two tables above for a period of 3750 days. The Figures (histograms) are the % components from V value bin (light grey) and G growth bin (dark grey) that have moved to above 50 ranking and below 50 rankings respectively. An average of nearly 50% value and growth components move above and below the 50 mean. This illustrates a case of Galtonian reversion using the Jiseki proxy. The section on the right hand side marked ‘Divergence’ is the number of components in the 40-60 Core ranking move toward 0-20 Value bin at the bottom extreme and 80-100 Growth at the top extreme. This case of Divergence illustrates that just like Reversion, there are components in the Jiseki proxy that illustrate divergence from the mean. The Reversion numbers are around 50% and are similar to the average 38% in case of Divergence. The summary illustration suggests that Jiseki proxy experiences both reversion and divergence, a classic expression in case of natural systems.
Testing Jiseki proxy for stationarity
Building further on the Jiseki Proxy we cite here a previous work done on stationarity on Proxy rankings. Researchers in Finance have long been interested in the long-run time-series properties of equity prices, with particular attention to whether stock prices can be characterized as random walk (unit root) or mean reverting (trend stationary) processes.
If stock price follows a mean reverting process, then there exists a tendency for the price level to return to its trend path over time. In their 1985 paper ‘Does the stock market overeact?”, DeBondt and Thaler explained the idea of mean reversion and how it leads to the Loser’s portfolio of 3 years outperforming the Winner’s portfolio of the same time. Findings of reversion in stock prices towards some fundamental values remain in literature for a decade. DeBondt and Thaler[1985] using overreaction showcased that a stock experiencing a poor performance over a 3-5 year of period subsequently tend to outperform that had previously performed relatively well. This implies that, on average, stocks which are ‘losers’ in terms of returns subsequently become ‘winners’ and vice versa.
In the paper, ‘Mean Reversion Indexing’, 2011, the author used the Jiseki proxy derived from the relative performance of the a group of 1000 assets and tested the Jiseki proxy for mean reversion and stationarity. The paper illustrated how Jiseki relative rankings derived from price not only exhibited stationarity, but also extended the absolute change of rankings from top down to the dynamic mean at 50 and vice versa. If stocks which are losers becoming winners that means they are showing the property of mean reversion. Fama and French (1988) also report mean reversion in U.S. equity market using long-horizon regressions, and Poterba and Summers (1988) document evidence of mean reversion using the variance ratio test. Instead of choosing the worst 3 year losers, the study tested the 1.5 year worst losers. The aim was to see if the mean reversion results can be simulated to a smaller (half) period.
Outlier performance in the last 5-6 years. The table above observes that 44% to 25% of the negative outliers witnessed outliers witnessed mean reversion tendency.
* < 20% means ranking less than 20%
* > 50% means ranking greater than 50%
Conclusion
Though Galton’s reversion is a robust law driving behavior and the study of behavior using statistics, mean reversion failure is also a reality. Galton laid down a framework for functioning of natural systems with a balance of reversion and diversion. He primarily focussed on illustrating reversion and did not build a case on divergence. Divergence is the missing element which could further enhance the definition of Galtonian natural system and explain why reversion failure is a reality. The paper builds a proxy ranking, by explaining how divergence could not just be noise, but the missing element in the definition of a natural system. The paper explains divergence as a relative performance case which can be extended from a pair of relative performance between two assets (index) prices to a ranking between a group of assets. In this paper the Jiseki proxy uses the stock market data and ranks components on a scale of 0 to 100 and then illustrates how the components among this proxy revert and diverge over different time durations and upto 38-50% above a 10 year period. The simplicity of the proxy makes it universal in working and further tests on data set across different non-Financial domains could establish it as a mean reversion framework, which allows for understanding divergence as a part of the reversion process.
Bibliography
Regression towards mediocrity in Hereditary Stature, Galton, 1886
Arsentis P., Paula L.F. – Financial Liberalization and Economic Performance in Emerging Countries, Palgrave Macmillian, New York, 2008 Beim, D.O., Calomiris C.W . – Emerging Financial Markets, McGraw Hill International Edition, Finance Series, 2001
Das., D.K. – Financial Globalization and the Emerging Market Economies, Routledge Studies in the Modern World Economy, 2004 Kolodko, G.W. – Emerging Market Economies (Globalization and Development), Ashgate Publishing Limited, England 2003
Reversion to the Mean, Taken to the Extreme, Jan H. Timmer, 2010
Mean Reversion of Size-Sorted Portfolios and Parametric Contrarian Strategies, Jeffrey Group, 2004 Mean Reversion in Stock
Prices: Evidence from Emerging Markets, Kaushik Chaudhari, 2004
A Mean-Reversion Theory of Stock-Market Crashes, Eric Hillebrand, 2003
Does the stock market overreact, De Bondt, Richard Thaler, 1985
Universality in Multi-Agent Systems , Parunak, H.V.D.; Brueckner, W.; Savit, R. (2004)
The Divergence Cyclicality; Pal, Nistor, 2011
The BRIC Model from a Japanese Perspective - Pre and Post Financial Crisis Review and Forecasts, Pal, Nistor, 2010
Mean Reversion Indexing, Pal, 2012